Solving Logical Business Problems Using Prolog: Part Three

In part one of this series, we reviewed the basics of Prolog programming. In part two, we learned about Constraint Logic Programming (CLP). In this part, we will use the knowledge we’ve gained in a program that automatically schedules employee assignments.

You can download the full program from GitHub. To run it, load it into the SWI-Prolog interpreter and type:

?- schedule(Schedule).

Given a set of employees, we want to assign each one to specific tasks at different shifts throughout the week. There are several restrictions we need to take into account:

1. Every task must have at least one employee assigned to it at every required shift.

2. No employee may be assigned to multiple tasks in the same shift.

3. No employee may be assigned to more than their maximum number of shifts (e.g., due to required 40-hour work weeks).

4. No employee may be assigned to a task during a shift in which they are unavailable (e.g., for PTO).

5. No employee may be assigned to a task for which they lack the necessary skills.

6. Any pre-existing employee assignments must be retained.

These are all common assignment restrictions, especially for jobs that must adhere to union rules.

We will reduce this scheduling problem to a boolean satisfiability problem, for which CLP is well suited. That is, our program will automatically generate a boolean expression that is satisfied if and only if the above constraints are fulfilled. Any satisfying assignment of variables for that sentence can then be directly translated to employee task assignments. Our general strategy is similar to that of this research paper for scheduling nurse assignments.

Each variable in our boolean sentence will represent an assignment of a specific employee to a specific task during a specific shift. To simplify things somewhat in our Prolog program, we treat each combination of a task and shift as a separate task pair task(TaskName, shift(Day,Time)). Therefore, the variable Aex,ty represents an assignment of employee x to task-shift pair y.

In Prolog we can keep track of our assignment variables using an association list, which is similar to a hash table in other languages. We start by finding every assignment combination of an employee to a task assign(E,T), associating each with a different unbound variable representing Aex,ty. Our program contains two utility predicates, assoc_keys_var(+Assoc,+Key,-Var) and assoc_keys_vars(+Assoc,+Keys,-Vars), which can be used to look up the unbound variables for one or multiple assignments, respectively.

Our main entry predicate is schedule(-Schedule). It begins by collecting all employees Es and tasks Ts, then it uses those to generate the assignment association list Assoc. Those are submitted as inputs to constraints(+Assoc,+Employees,+Tasks), which generates constraints to define the world of all valid employee assignments. Once the constraints are declared, the clpfd predicate label non-deterministically assigns working truth values to each assignment. Finally, a findall collects all assignments that have been set to true (1), returning those as the output Schedule.

We are most interested in the constraints predicate. For this program we’ve separated the concerns of our 6 requirements above into 6 separate predicates, each called in turn by constraints:

constraints(Assoc,Es,Ts) :- core_constraints(Assoc,Es,Ts), simul_constraints(Assoc,Es,Ts), max_shifts_constraints(Assoc,Es,Ts), unavailable_constraints(Assoc,Es,Ts), skills_constraints(Assoc,Es,Ts), assigned_constraints(Assoc).

Note that constraints does not actually set any output variables. Each predicate it calls uses the same employee assignment variables to define our constraints, which are collected by the CLP engine to infer satisfying values. If we were ever to create a new rule for employee assignments, we could easily implement it as a new predicate and add it here.

We begin with core_constraints, which generates the constraints for our first requirement: that each task must have at least one employee assigned to it. Logically, our Boolean sentence will be of the following form (note that ∧ represents “and” while ∨ represents “or”):

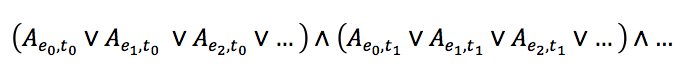
Note that we do not need to build the “and” operators into any of our logic directly, as conjunction in clpfd is implicit when collecting constraints. Therefore we really just need to create the disjunctive “or” sub-expressions:

% core_constraints(+Assoc,+Employees,+Tasks) core_constraints(Assoc,Es,Ts) :- maplist(core_constraints_disj(Assoc,Es),Ts).   % core_constraints_disj(+Assoc,+Employees,+Task) core_constraints_disj(Assoc,Es,T) :- findall(assign(E,T),member(E,Es),Keys), assoc_keys_vars(Assoc,Keys,Vars), list_or(Vars,Disj), Disj.

The main core_constraints predicate utilizes a helper predicate core_constraints_disj to create our disjunctive constraints. The built-in Prolog predicate maplist is used here to call core_constraints_disj once for each task in the program database, where each call sets the first two parameters to Assoc and Es, and the third to the next task in Ts. In core_constraints_disj, we use findall to collect all assignment pairs Aex,T for all employees ex and a given task T. Once we have the Prolog variables associated with each such assignment, we combine them into a single large disjunctive expression (Ae0,T ∨ Ae1,T ∨ …) using a simple utility predicate list_or. Finally, we state the new disjunctive constraint expression Disj directly, automatically submitting it to the clpfd engine.

Next is simul_constraints, which prevents an employee from being assigned to multiple tasks during the same shift. We have implemented this using arithmetic constraints that take advantage of each assignment variable being assigned as either 0 (false) or 1 (true):

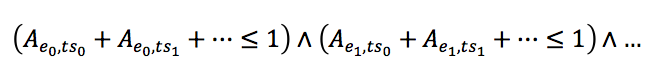
Here, ts0, ts1, etc. denote tasks that occur during the same shift, and the above expression is repeated for each different shift. We implement these constraints with the following code:

% simul_constraints(+Assoc,+Employees,+Tasks) simul_constraints(Assoc,Es,Ts) :- shifts(Shifts), findall(employee_shift(E,Shift), (member(E,Es),member(Shift,Shifts)),EmployeeShifts), maplist(simul_constraints_subexpr(Assoc,Ts),EmployeeShifts).% simul_constraints_subexpr(+Assoc,+Tasks,+EmployeeShiftPair) simul_constraints_subexpr(Assoc,Ts,employee_shift(E,Shift)) :- findall(task(TName,Shift),member(task(TName,Shift),Ts),ShiftTs), findall(assign(E,T),member(T,ShiftTs),Keys), assoc_keys_vars(Assoc,Keys,Vars), sum(Vars,#=<,1).

The simul_constraints predicate collects all employee-shift pair combinations employee_shift(E,Shift), then uses maplist to call the helper predicate simul_constraints_subexpr for each pair. There we build each arithmetic constraint sub-expression by collecting all tasks associated with the given shift and all variables assigning the given employee to any task during that shift. Finally, we use sum to generate a constraint requiring all of those variables to add up to a value less than or equal to 1, effectively requiring at most one of them to be assigned “true”.

The max_shifts_constraints predicate, which prevents an employee from being assigned to too many shifts, is similar, and can be represented by the following expression:

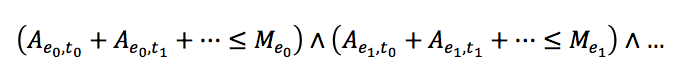
Here, Mex is the maximum number of shifts to which employee ex can be assigned. In the code, each arithmetic sub-expression is represented using sum(Vars,#=<,MaxShifts).

The remaining three constraint predicates unavailable_constraints (no employee may be assigned to a task during a shift in which they are unavailable), skills_constraints (no employee may be assigned to a task if they lack the necessary skills), and assigned_constraints (any pre-existing task assignments must still hold) all directly assign values to the appropriate variables. In each case, we collect the relevant variables Vars using findall, and then set them all to Value (0 with the first two constraints, 1 with the third) using maplist(#=(Value),Vars). The code for these predicates is generally straightforward, so we will not review them further here.

Conclusion

Constraint Logic Programming is exceptionally useful for concisely solving scheduling problems. The logic for our employee scheduler fits entirely within less than 200 lines of Prolog code! Moreover, it is easy for us to add new constraints for new rules by creating and adding new predicates.

This program would normally just be used to obtain a single valid assignment schedule. However, because of Prolog’s non-deterministic nature, the program can technically return all possible schedules. If no schedule fits the desired parameters, the scheduler will simply fail.

In Part 4 of this series, we will show how to use a Java program to call this Prolog program to retrieve a schedule and then process its results.

Special thanks to Markus Triska for his extremely helpful advice during the development of this scheduling program.

 Micah Jones is a consultant in Credera’s Integration & Data Services (IDS) practice. In 2011, he received his doctorate in computer science from the University of Texas at Dallas, specializing in programming language-based security.

Photo Cred: https://fossbytes.com/what-is-programming-and-why-you-should-learn-to-code/

• Prolog